Bir Fransız matematikçi tarafından, tüm dışbükey beşgenlerin ve dolayısıyla düzlemi döşeyen tüm dışbükey poligonların sınıflandırmasını sağlayan bir problem ortaya konulmuştu

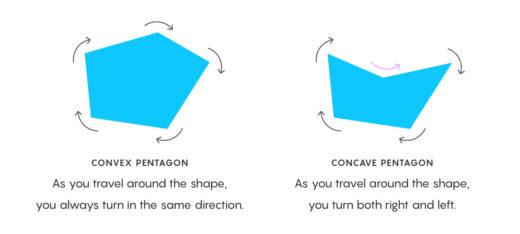
Geometrinin en eski problemlerinden birisi; sonsuz bir düzlemi kapsayacak şekilde mozaik olarak adlandırılan desenler ile ve kopyaları ile mozaiklemek, kaplamaktır. M.C. Escher’in mozaik kertenkele ve diğer yaratıklardaki çizimlerindeki sınırsız şekil çeşitliliğinin bunu yapabileceğini göstermektedir. Sınıflandımanın sınırlı olmasına rağmen, Poliganlar açıları aynı yönde bükülen üçgenler ve dikdörtgenler gibi basit, düz kenarlı şekillerdir.
Şimdi, CNRS’de (Fransa’nın bilimsel araştırma merkezi) 37 yaşındaki bir matematikçi olan Michaël Rao’nun yeni bir kanıtı ile sonunda 99 yıldır sıralanamayan sınıflara aykırı beşgenler olan ve düzlemi döşeyen dışbükey poligonların sınıflandırması sağlandı
Düzenli beşgenleri – eşit açılı ve yanlara sahip olanlar- düzleme yerleştirmeyi deneyin; döşeme, mozaiklemeyi sağlayamazsınız. Antik Yunanlılar kiremitli tek poligonların üçgen, dörtgen ve altıgen olduğunu kanıtladı. (çoğu banyo zemininde görüldüğü gibi) Fakat bir beşgeni düzensiz bir şekle sokup gerdiğinizde bozulmalar meydana hale gelir
1918’de Alman matematikçi Karl Reinhardt, doktora tezi olarak düzlemi döşemek için düzensiz dışbükey beşgen tipleri belirledi: Bunlar, “a kenarı = b kenarı,” “c = d” ve “A ve C açılarının her ikisi de 90 dereceye eşit.” gibi ortak kurallar tarafından tanımlanan gruplar, ailelerdi.
Reinhardt, beş ailesinin bu listeyi tamamlayıp tamamlamadığını bilmiyordu ve ilerleme 50 yıl durdu. Daha sonra, Johns Hopkins Üniversitesi’nden Richard Kershner, 1968’de, konveks dışbükeylere ait üç tür daha keşfetti ve bunlardan başkalarının olmadığını kanıtladığını iddia etti. Fakat Kershner’in yazısı kanıtın dışına çıktı. “Mükemmel nedenden ötürü” ifadesinin olduğu bir giriş notu okurken, “Tam bir kanıt, oldukça büyük bir kitap gerektirir” dedi.
Kershner’in Beşgen iddiası ile ilgili haberler, Martin Gardner’ın Scientific American’daki popüler matematik sütununda ortaya çıkınca 1975’de kitlelere yayıldı. Ancak kısa süre sonra, San Diego’da lise matematik eğitimi alan bir ev hanımı olan Marjorie Rice gibi okuyucular, Kershner tarafından bilinenlerin dışında yeni mozaik oluşturma beşgen aileleri keşfetti (4 adet). Ailelerin listesi 13’e, 1985’te ise 14’e yükseldi. Washington’daki Bothell Üniversitesi’nden matematik doçenti olan Casey Mann ve yardımcıları, 2015’te 15 inci dışbükeyi keşfetmek için bir bilgisayar araması yaptılar.
Rao, Mann ve ekibinin keşfini duyduğunda, konveks beşgenlerin sınıflandırmasını bir kerede ve tamamıyla tamamlayacak kapsamlı bir araştırma yapmak için yola çıktı.
Bilgisayar destekli yeni kanıtı Rao, beşgenlerin köşelerinin bir fayans döşeme biçiminde nasıl bir araya gelebileceğine dair 371 olası senaryo tespit etti ve hepsini kontrol etti. Sonunda, onun algoritmasını yalnızca bilinen 15 beşgen ailesinin yapabileceğini belirledi. Onun kanıtı, düzlemi döşeyen dışbükey poligonların alanını 15 beşgen ve üç tip altıgen kapattığını ortaya koyuyordu (Reinhardt’ın 1918 tezinde hepsi tanımlanmıştı) .
Mann, Fransa’daki gelişmeleri duyduğu zaman, kendisinin ve yardımcılarının kapsamlı bir kanıta doğru kısmi bir adım atmaya çalıştıklarını söyledi.
Geometri problemlerini çözmek için bilgisayar yazılımları kullanımında lider konumunda bulunan Pittsburgh Üniversitesi’nden matematik profesörü Thomas Hales, bağımsız olarak Rao ispatının en önemli kısmını tekrar ortaya koydu ve bir hata olmadığını belirtti. Rao’nun yine de emsal gösterilen yayınlar için bir ispat sunması gerekiyor ama Thomas Hales çoktan kendinden emin olduğunu hissediyor.
İspatında, Rao ilk olarak dışbükey beşgen köşelerinin nasıl bir araya gelebileceği konusunda sınırlı miktarda senaryo olduğunu ortaya koydu; fakat bu senaryoların kontrol edilmesi gerekiyordu. Bir beşgenin köşelerine kısıtlamaların hangi şekilde getirilmesi konusunda basit geometrik koruma yasalarını kullandı. – 1 den 5 e kadar etiketli – bir döşemede muhtemel köşelerde buluşabilir. Bu koşullar, 1’den 5’e kadar olan açıların toplamının herhangi bir beşgen için toplam olan 540 dereceye eşit olması ve beşinin her beş köşeli karonun bir parçası olması nedeniyle beşinin eşit derecede bir döşeme işine katılmaları gerektiğini içermektedir. Ancak, belirli bir köşedeki açıların toplamı, eğer bitişik beşgenlerin köşeleri bu noktada buluşursa 360 derecedir lakin bazı köşeler başka bir beşgenin kenarı boyunca buluşursa 180 derecedir.
Bu tür kuralları uygulayarak, Rao, 371 senaryonun haricinde, “Ya açı denklemleri ya da yüzdeler kendi kendini çelişiyor” dedi Kaliforniya Üniversitesinde matematik profesörü olan Greg Kuperberg. Rao’nun muhtemel açı koşulları setlerini yazdığı gibi, sınırlı sayıda “iyi set” garantisi yoktur, Kuperberg, “Ancak bu bilgisayar çalışması iyi sonuçlar verdi” dedi.
İspatında iki ana aşamadan ikincisinde, Rao, güzel setleri birer birer geçti ve bu açı koşullarını karşılayan herhangi bir karonun var olup olmadığını kontrol etti. Kodlamaya geldiğinde, “daha karmaşık bir bölüm”, dedi Rao. Kuperberg, “371 senaryonun her biri için,” algoritması, yalnızca izin verilen köşe yapılandırmalarını kullanarak bir kerede bir döşeme bırakarak bir döşeme parçasını birleştirmeye çalışıyor “dedi.
Bu 371 ağaç ihtimalini araştırırken, algoritma ya bir ağacın her yolunun 15 bilinen aileden birinde bir beşgen oluşturduğunu belirledi ya da “ağaçtaki tüm yollar sonlu sayıda adımdan sonra çıkmaza çıkıyor” diyor Brown Üniversitesi’nde ilgili problemler hakkında çalışmalar yürüten bir matematikçi olan Rich Schwartz.
Rao, içbükey şekillerin konveks olanlardan daha büyük bir kombinasyonel problemi temsil ettiğini belirtmesine rağmen, algoritmalarını einstein’ın izinde tutmayı planlıyor
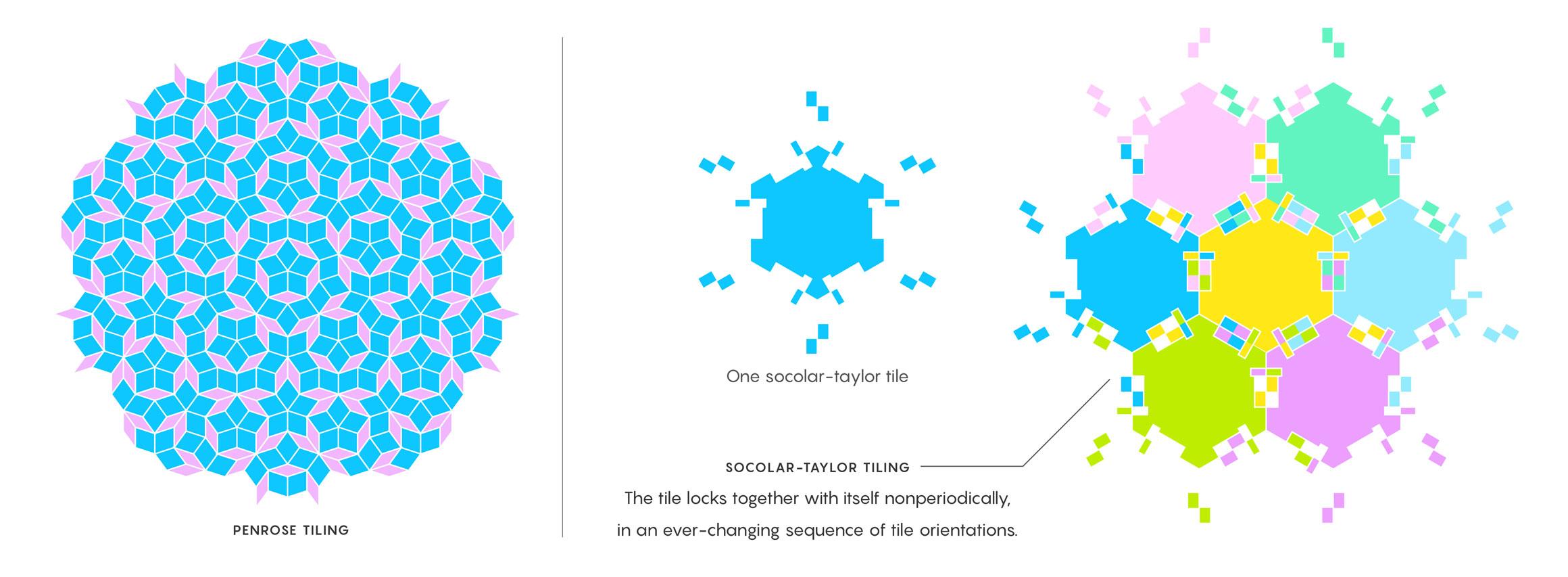
Son zamanlarda, Rao ve bir yardımcısı, Wang fayanslarının periyodik olmayan yatakları hakkında farklı bir sonuç elde ettiğini kanıtladılar – renk kenarı sadece renklerin eşleşmesi halinde yan yana yerleştirilebilen kareler.
Önceki çalışma, Wang kiremit koleksiyonlarının yalnızca periyodsuz olmayan eğilimler oluşturduğu kanıtlamıştı. Mann, “İlk bulunanlarda 20.000’in üzerinde fayans vardı” dedi. “Daha sonra 14’e düşürüldü. Rao, minimum 11 karo ile yapabildiğini kanıtladı















